Chapter 05 : DES 算法和 AES 算法¶
约 1668 个字 30 行代码 14 张图片 预计阅读时间 9 分钟
DES 算法¶
DES(Data Encryption Standard)是一种对称密钥加密算法,采用大端序存储数据,明文和密钥均为 64 位
加密过程¶
DES 算法的加密过程包括以下几个步骤:
- 首先对 64 位的明文进行初始置换,得到一个 64 位的中间结果
- 中间结果的 8 字节会被分成左边 4 字节和右边 4 字节,在 DES 框架代码中分别表示为 \(L[0],R[0]\)
- 第 0 轮循环先对 \(L[0]\) 加密,生成 \(L[1]\);\(R[0]\) 不作改变直接赋值给 \(R[1]\)
- 第 1 轮循环先对 \(R[1]\) 加密,生成 \(R[2]\);\(L[1]\) 不作改变直接赋值给 \(L[2]\)
- 如此反复得到最后的 \(L[16],R[16]\),最后进行初始置换的逆置换得到密文
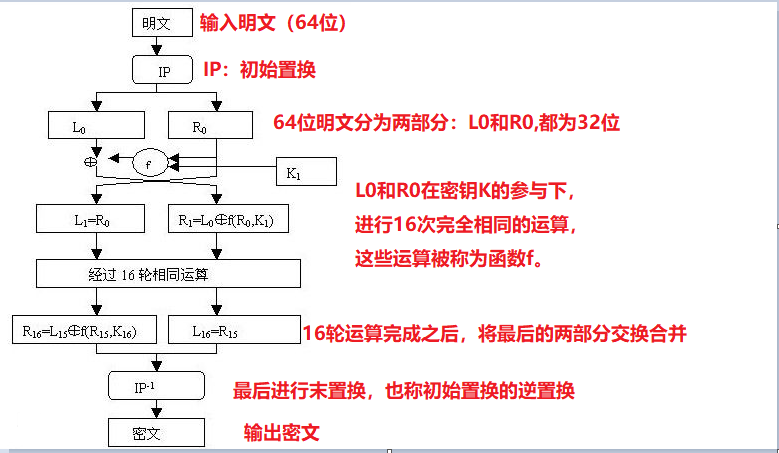
其中,初始置换的转换表如下:

对于其中的加密过程,即图中的函数 \(f\),可以分为密钥处理、扩展子块、 SBOX 替换三个步骤:
密钥处理¶
先对密钥进行处理:
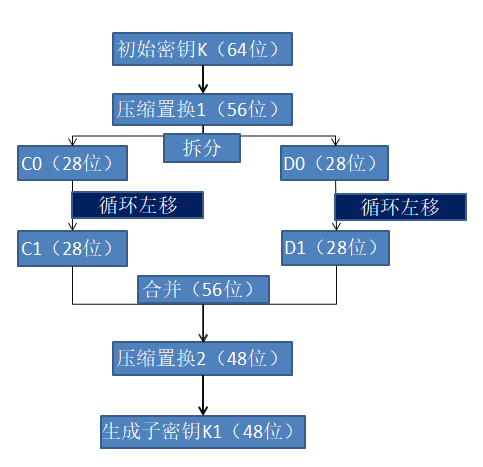
压缩置换 1 是将 64 位的密钥压缩成 56 位,本质是原密钥的拆分重组,转换表如下:

每个子密钥的循环左移次数如下:

压缩置换 2 的转换表如下:

扩展子块¶
因为我们生成的密钥为 48 位,因此我们还需要将加密的 32 位扩展成 48 位方便异或操作,扩展表如下:

SBOX 替换¶
将压缩后的密钥和扩展后的子块异或之后,我们得到了一个 48 位的中间结果。接下来我们需要将这个中间结果分成 8 个 6 位的子块,然后对每个子块进行 SBOX 替换,得到 32 位的输出。SBOX 对应也有 8 个,第一个的转换表如下:
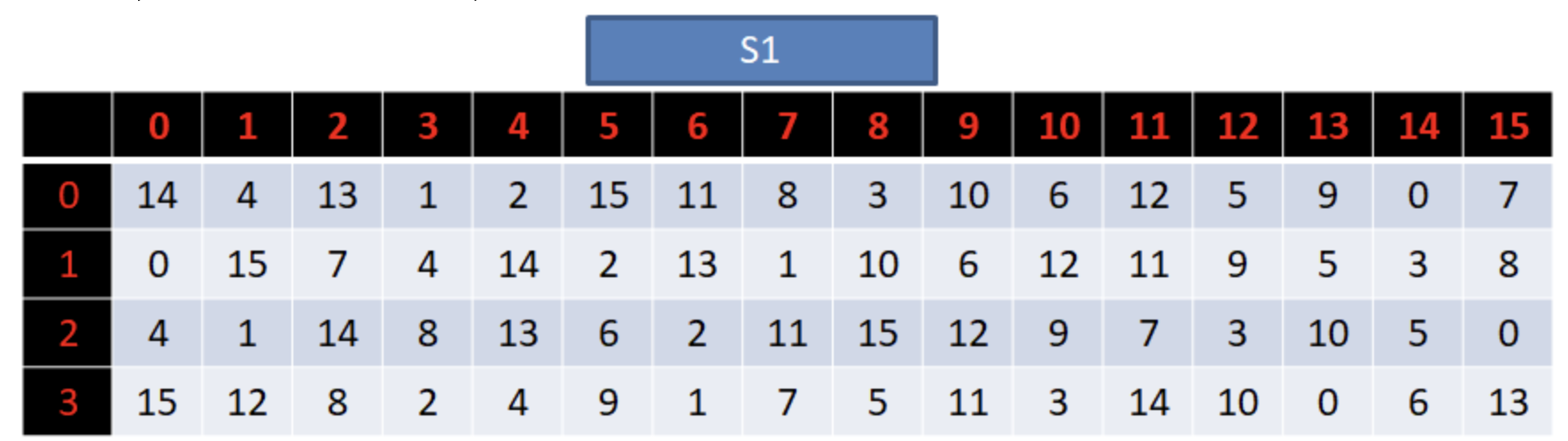
对于输入的 6 位中间结果,我们取第一位和最后一位拼成一个两位二进制数字表示行号,中间四位二进制数字表示列号,对应的 SBOX 中的结果即为替换后的结果,所有 8 个 SBOX 生成替换结果拼起来即为替换结果
缺点¶
DES 有如下缺点:
- 密钥长度太短
- 利用差分分析可以攻击 DES 算法
- SBOX 没有公开,怀疑有后门
AES 算法¶
AES(Advanced Encryption Standard)是一种对称密钥加密算法,明文为 128 位,密文为 128 位,密钥长度有 128 位、 192 位和 256 位三种长度
数学基础¶
有限域¶
域 \(F\) 记作 \(\{F,+,*\}\) ,是一个拥有两个运算的集合,这两个运算分别称为加法和乘法。本质上说,域就是一个集合,我们可以在上面做加减乘除运算而不脱离该集合
- 有限域中元素的个数称为有限域的阶(Order)
- 有限域的阶必为素数 \(p\) 的幂,即 \(p^n\),其中 \(n\) 为正整数
- 对任意素数 \(p\) 和正整数 \(n\),都存在一个有限域的阶为 \(p^n\) 的有限域,记为 \(GF(p^n)\)。当 \(n=1\) 时,\(GF(p)\) 也称素域
有限域 \(GF(p)\)¶
给定一个素数 \(p\),元素个数为 \(p\) 的有限域 \(GF(p)\) 定义为整数 \(\{0,1,2,\cdots,p-1\}\) 的集合 \(Z_p\),其运算为\(\text{ mod }p\) 的算术运算
最简单的有限域是 \(GF(2)\),该有限域的元素的个数为 2,它们分别是 0 和 1,在 \(GF(2)\) 上的加法运算等价于异或运算,乘法运算等价于二进制与运算
Example


有限域 \(GF(2^8)\)¶
- 对于 \(F[x]\) 中的每个不可约多项式 \(p(x)\),可以构造一个域 \(F[x]_{p(x)}\)
-
设 \(p(x)\) 是 \(F[x]\) 中 \(n\) 次不可约多项式,令 \(F[x]_{p(x)}\) 为 \(F[x]\) 中所有次数小于 \(n\) 的多项式集合,即:
\[ F[x]_{p(x)}=a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots+a_{1}x+a_{0} \]其中 \(a[i]\in F\),即在集合 \(\{0,1,2,\cdots,p-1\}\) 上取值,则我们可以定义 \(F[x]_{p(x)}\) 上的加法运算及乘法运算如下:
\[ \begin{aligned} a(x)+b(x)&=(a(x)+b(x))\text{ mod } p(x)\\ a(x)*b(x)&=(a(x)*b(x))\text{ mod } p(x) \end{aligned} \] -
在 \(GF(2^n)\) 中,\(F[x]_{p(x)}\) 中所有次数小于 \(n\) 的多项式可以表示为:
\[ f(x)=a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots+a_{1}x+a_{0} \]其中系数 \(a_{i}\) 是二进制数,该多项式可以由它的 \(n\) 个二进制系数唯一表示。因此 \(GF(2^n)\) 中的每个多项式都可以表示成一个 \(n\) 位的二进制数
-
AES 算法选择用多项式表示有限域 \(GF(2^8)\) 中的元素,其中不可约多项式 \(p(x)\) 为 \(x^8+x^4+x^3+x+1\),该多项式对应的二进制数为 100011011,对应的十六进制数为 0x11B。AES 算法的 MixColumn 步骤中对两个 8 位数做乘法运算时必须\(\text{ mod}\) 0x11B
- AES 算法的 MixColumn 步骤中还涉及 3 次多项式的乘法,多项式乘法运算必须\(\text{ mod } x^4+1\),目的是使得乘积仍旧为一个 3 次多项式,例如:\(x^6 \text{ mod } (x^4+1) = ((x^4+1)x^2 - x^2)\text{ mod }(x^4+1)=-x^2=x^2\text{ mod }(x^4+1)\)
- AES 加密及解密分别使用以下两个多项式作为被乘数:
- 加密:\(3x^3+x^2+x+2\)
- 解密:\(0x0B x^3+0x0D x^2+0x09 x+0x0E\)
- AES 加密及解密分别使用以下两个多项式作为被乘数:
MixColumn 中的 8 位数乘法运算
算法流程¶
以 128 位(16 字节)密钥为例,设 \(p\) 为明文,\(k\) 为密钥,则 AES 的加密过程如下:
其中,ShiftRow 函数表示对明文 16 字节构成的 \(4\times 4\) 矩阵逐行做循环左移:

sbox 的生成步骤为 \(\text{sbox}[a] = (((a^{-1}\text{ mod }0x11B)*0x1F)\text{ mod }0x101) \oplus 0x63\)
对 MixColumn,具体步骤如下:
- 对 \(4\times 4\) 的矩阵 \(m\) 中的 4 列与 \(a\) 做在有限域 \(GF(2^8)\) 多项式模 \((x^4+1)\) 的乘法运算
- 加密时采用的被乘数 \(a\) 为多项式 \(3x^3+x^2+x+2\),用数组表示为
unsigned char a[4]={0x03, 0x01, 0x01, 0x02}; - 解密时采用的被乘数 \(a\) 为加密所用多项式的逆,即
{0x0B, 0x0D, 0x09, 0x0E}
- 加密时采用的被乘数 \(a\) 为多项式 \(3x^3+x^2+x+2\),用数组表示为
- 乘法所得 4 列转成 4 行并保存
密钥生成¶
以 128 位种子密钥为例,假定机器存储模式为大端序(高字节在前,低字节在后),设 long k[4] 为种子密钥,则后面还需要生成 k[4] 至 k[43] 共 40 个 long,步骤如下:

以上过程生成了 4 个 long,是一组 16 字节的 key,同理生成 k[8] 至 k[11]

